At Studit, we believe learning geometry should be fun and straightforward, just like a 180-degree angle! Whether you’re a Class 6 student exploring angles for the first time or a Class 10 student preparing for board exams, understanding the 180-degree angle is a key step in mastering geometry. Let’s dive into what a 180-degree angle is, how to measure and draw it, and why it matters for your studies!

What is a 180-Degree Angle?

A 180-degree angle is called a straight angle because it forms a perfect straight line. Imagine stretching your arms out wide to make a straight line—that’s what a 180-degree angle looks like! In geometry, angles are classified based on their size, and here’s a quick guide to help you remember:

• Acute Angle: Less than 90° (think sharp and small, like a slice of pizza!)
• Right Angle: Exactly 90° (like the corner of your notebook)
• Obtuse Angle: More than 90° but less than 180° (a bit wider than a right angle)
• Straight Angle: Exactly 180° (a straight line, like a ruler)
• Reflex Angle: More than 180° but less than 360°
• Full Rotation: Exactly 360° (a complete circle, like spinning around!)

The 180-degree angle is special because it’s the angle you see when two lines form a straight path, like a road stretching out in front of you.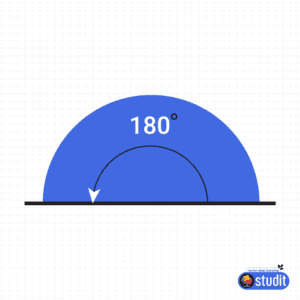

Why is the 180-Degree Angle Important?

Understanding the 180-degree angle is key for solving geometry problems, especially in topics like triangles and supplementary angles. For example, did you know that the sum of all interior angles in a triangle always equals 180 degrees? Or that two angles that add up to 180 degrees are called supplementary angles? These concepts are crucial for CBSE, ICSE, and state board exams, and Studit’s expert tutors are here to help you master them!

How to Measure a 180-Degree Angle Using a Protractor

Measuring a 180-degree angle is easy with a protractor. Follow these steps, and you’ll be a pro in no time: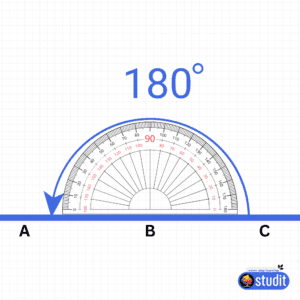

1. Draw a Straight Line: Use a ruler to draw a straight line on your paper. Label one end as point A and the other as point B.
2. Mark the Vertex: Place a dot anywhere on the line (let’s call it point O). This is the vertex of your angle.
3. Align the Protractor: Place the center of the protractor on point O, making sure the baseline of the protractor lines up with the line (A to B).
4. Find 180°: Look at the protractor’s scale. The 180° mark should align perfectly with the straight line, confirming it’s a straight angle!

With Studit’s personalized tutoring, our teachers can guide you step-by-step, whether you’re practicing in-person or through our app.

How to Draw a 180-Degree Angle Using a Compass

Don’t have a protractor? No problem! You can draw a 180-degree angle using a compass. Here’s how: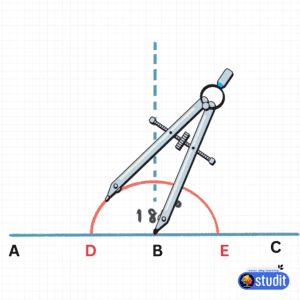

1. Draw a Line: Use a ruler to draw a straight line and label it XY.
2. Mark a Point: Choose a point on the line (call it O).
3. Draw an Arc: With point O as the center, use a compass to draw an arc that crosses the line on both sides (label these points P and Q).
4. Check Your Angle: The angle formed by points P, O, and Q is 180 degrees because it lies on a straight line.

Want to practice this with a tutor? Book a free demo class with Studit, and we’ll help you perfect your compass skills!

Fun Facts About the 180-Degree Angle

• It’s Everywhere!: Look around—you’ll see 180-degree angles in straight roads, the edge of a table, or even when you stretch a rubber band tight.
• Supplementary Angles: If one angle is 70°, its supplementary angle (which adds up to 180°) is 110°. Try this with any angle pair!
• Triangles and 180°: The sum of angles in any triangle is always 180°. This is a must-know for geometry exams!

Try These Practice Questions

Q.1: If a right angle is divided into two parts and one part measures 30°, find the other angle.

Solution:
Let the unknown angle be x
Right angle = 90°
Given one angle = 30°

So,
x + 30 = 90
x = 90 – 30 = 60°

Answer: The other angle is 60°

Q.2: Two angles form a linear pair. One of them is 110°. Find the other.

Solution:
Linear pair angles are supplementary (sum = 180°)
Let the other angle be x

x + 110 = 180
x = 180 – 110 = 70°

Answer: The other angle is 70°

Q.3: If two complementary angles are equal, find the value of each.

Solution:
Complementary angles add up to 90°
Let each angle be x

x + x = 90
2x = 90
x = 90 ÷ 2 = 45°

Answer: Both angles are 45°

Q.4: One angle is 3 times its complement. Find both angles.

Solution:
Let the complement be x, so the other angle is 3x
x + 3x = 90
4x = 90
x = 22.5°, 3x = 67.5°

Answer: The angles are 22.5° and 67.5°

Need help solving these? Studit’s tutors can explain these problems in a way that makes sense to you, whether you’re in Class 5 or Class 12.

Learn Geometry with Studit!

At Studit, we make geometry exciting and easy to understand. Our expert tutors in Bhubaneswar provide personalized home tuition and online classes to help you master angles, triangles, and more. With the Studit app, you can track your progress, book sessions, and even try a free demo class to see how we can help you shine in math!

Ready to conquer geometry? Visit www.studit.in or download the Studit app to get started today. Let’s make learning as straight as a 180-degree angle!